알고리즘 문제 풀이 / 프로그래머스 (programmers) - 멀쩡한 사각형

문제 링크
https://programmers.co.kr/learn/courses/30/lessons/62048
코딩테스트 연습 - 멀쩡한 사각형
가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을
programmers.co.kr
문제 풀이
최대공약수를 먼저 구한다.
x좌표 + y좌표 - 1 이란 공식을 생각한다.
전체 사각형에서의 직각삼각형을 보고 있자니 같은 비율의 최소 직각삼각형에서의 길이를 구한 후, 그 배수만큼 곱하면 되겠단 생각이 먼저 들었다. 쉽게 말해서 최대공약수를 곱하면 되는거였다.
두번째로 생각해야 할 것은 최소인 직각삼각형에서의 빗변이 지나가는 직사각형이 몇개인지를 알아야하는데 이게 어려웠다.
규칙을 찾기 위해서 피타고라스의 정의, 가로세로의 곱 등등 이것저것을 생각해보다 찾은 규칙은 좌표인데 그림과 함께 설명해보자면
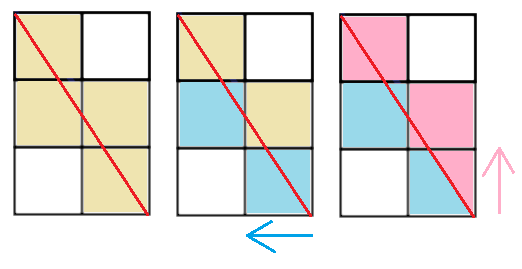
먼저 x좌표로 갈 수 있는 칸을 체크하고, y 자표로 갈 수 있는 거리를 체크하면 된다. 이 때, 맨 처음에는 둘 다 거치게 되므로 1을 빼주는 방식으로 풀었다. 처음엔 이게 우연인가 싶어서 혼자 그림을 더 그려보면서 많은 경우를 비교해보아도 다 맞았다.
이렇게 풀었을 때, 테스트 12 ~ 17번이 틀린것으로 나왔다. 아무리 생각해도 이 코드가 틀릴 수 없다고 생각했다.
그러다 혹시나 놓친게 있을까 하고 문제를 다시 읽어보는데 제한사항에 " W, H : 1억 이하의 자연수 " 라는게 있었다. 그래서 모든 문자형을 int 에서 long으로 바꿔줬더니 정답이였다. 나는 항상 내가 무조건 맞다는 착각에 빠지는 경우가 많은데 이 버릇을 고쳐야겠다는 생각을 다시금 하게 됐다. 문제는 나름 금방 풀고 쉬운편이란 생각을 했는데 점수를 12점이나 줘서 놀랐다.
public static long solution(long w, long h) { // 문제에서는 int로 되어있는데 형 변환 해줘야 한다.
long min_w = w;
long min_h = h;
long min = -1;
while(min_w != 0) {
if(min_w < min_h) {
long num = min_w;
min_w = min_h;
min_h = num;
}
min_w -= min_h; // h가 최대공약수
}
min = min_h;
min_w = w / min;
min_h = h / min;
long answer = (long) (w * h - ( min_w + min_h - 1 ) * min);
return answer;
}
'Algorithm > Programmers' 카테고리의 다른 글
| [프로그래머스(programmers)] (2017 팁스타운) 예상 대진표 (0) | 2021.06.01 |
|---|---|
| [프로그래머스(programmers)] (2017 팁스타운) 짝지어 제거하기 (0) | 2021.05.29 |
| [프로그래머스(programmers)] (2019 KAKAO BLIND RECRUITMENT) 오픈채팅방 (0) | 2021.05.27 |
| [프로그래머스(programmers)] (Lv2) 124 나라의 숫자 (0) | 2021.05.26 |
| [프로그래머스(programmers)] (Lv3) 여행경로 (1) | 2021.05.21 |




댓글